Assalamualaikum warohmatulohi wabarakatuh

A. Pengertian Trigonometri

Trigonometri adalah fungsi yang menghubungkan besar sudut dengan perbandingan sisi-sisi segitaga siku-siku. Nilai perbandingan ini digunakan untuk menentukan besar sudut atau panjang sisi suatu segitiga. Konsep Trigonometri dikembangkan menjadi aturan sinus dan kosinus sehingga perbandingan trigonometri dapat berlaku untuk semua jenis segitiga.

b.Rumus Trigonometri Penjumlahan dan Selisih Dua Sudut

1. Rumus Cosinus Jumlah dan Selisih Dua Sudut

Untuk memahami rumus cosinus perhatikan gambar di bawah. Dari lingkaran yang berpusat di O(0, 0) dan berjari-jari 1 satuan :

Dengan mengingat kembali tentang koordinat Cartesius, maka:
a. koordinat titik A (1, 0)
b. koordinat titik B (cos A, sin A)
c. koordinat titik C {cos (A + B), sin (A + B)}
d. koordinat titik D {cos (–B), sin (–B)} atau (cos B, –sin B)
AC = BD maka AC2 + DB2
{cos (A + B) – 1}2 + {sin (A + B) – 0}2 = {cos B – cos A}2 + {–sin B – sin A}2
cos2 (A + B) – 2 cos (A + B) + 1 + sin2 (A + B) = cos2 B – 2 cos B cos A + cos2 A +
sin2 B + 2 sin B sin A + sin2 A
2 – 2 cos (A + B) = 2 – 2 cos A cos B + 2 sin A sin B
2 cos (A + B) = 2 (cos A cos B – sin A sin B)
cos (A + B) = cos A cos B – sin A sin B

mari kita simak rumus jumlah dan selisih dua sudut sinus dan cosinus beserta pembuktiannya.

Rumus Jumlah dan Selisih Dua Sudut

Rumus Jumlah dan Selisih Sudut Cosinus

Rumus Jumlah Sudut Cosinus

Rumus Jumlah Dua Sudut Cos Bukti:
Perhatikan gambar berikut!

Pembuktian Rumus Jumlah Sudut Cos

Titik koordinat A dan B di atas diperoleh berdasarkan fungsi sinus dan cosinus. Selanjutnya perhatikan titik M yang ditransformasi dengan besar sudut putar $\beta$ dan sudut pusat O dari titik A. Dan perhatikan titik N yang ditransformasi dengan besar sudut putar $- \beta$ dan sudut pusat O dari titik P. Untuk lebih jelasnya perhatikan gambar di bawah.

INGAT!!!

$cos (-\alpha) = cos \alpha$

$sin (-\alpha) = - sin \alpha$

Persamaan 1: Menghitung jarak P(1,0) ke M (cos $( \alpha + \beta)$ , sin $( \alpha + \beta)$ )

$\left| PM \right| = \sqrt{\left( x_{P} - x_{M} \right)^{2} + \left( y_{P} - y_{M} \right)^{2}}$

$\left| PM \right| = \sqrt{\left( 1 - cos \left( \alpha + \beta \right) \right)^{2} + \left( 0 - sin \left( \alpha + \beta \right) \right)^{2}}$

$\left| PM \right| = \sqrt{1 - 2cos \left( \alpha + \beta \right) + cos^{2} \left( \alpha + \beta \right) + sin^{2} \left( \alpha + \beta \right)}$

$\left| PM \right| = \sqrt{1 - 2cos \left( \alpha + \beta \right) + 1}$

$\left| PM \right| = \sqrt{2 - 2cos \left( \alpha + \beta \right)}$

Persamaan 2: Menghitung jarak A $(cos \alpha, sin \alpha)$ ke N $(cos \beta, -sin \beta)$

$\left| AN \right| = \sqrt{\left( x_{A} - x_{N} \right)^{2} + \left( y_{A} - y_{N} \right)^{2}}$

$\left| AN \right| = \sqrt{\left( cos \alpha - cos \beta \right)^{2} + \left( sin \alpha - (-sin \beta) \right)^{2}}$

$\left| AN \right| = \sqrt{\left( cos \alpha - cos \beta \right)^{2} + \left( sin \alpha + sin \beta \right)^{2}}$

$\left| AN \right| = \sqrt{cos^{2} \alpha - 2cos \alpha cos \beta + cos^{2} \beta + sin^{2} \alpha + 2sin \alpha sin \beta + sin^{2} \beta}$

$\left| AN \right| = \sqrt{cos^{2} \alpha + sin^{2} \alpha + cos^{2} \beta + sin^{2} \beta} + - 2cos \alpha cos \beta + 2sin \alpha sin \beta$

$\left| AN \right| = \sqrt{1 + 1 - 2cos \alpha cos \beta + 2sin \alpha sin \beta}$

$\left| AN \right| = \sqrt{2 - 2cos \alpha cos \beta + 2sin \alpha sin \beta}$

Secara geometri, persamaan 1 sama dengan persamaan 2, sehingga:

$\left| PM \right| = \left| AN \right|$

$\sqrt{2 - 2cos \left( \alpha + \beta \right)} = \sqrt{2 - 2cos \alpha cos \beta + 2sin \alpha sin \beta}$

$2 - 2cos \left( \alpha + \beta \right) = 2 - 2cos \alpha cos \beta + 2sin \alpha sin \beta$

$- 2cos \left( \alpha + \beta \right) = - 2cos \alpha cos \beta + 2sin \alpha sin \beta$

$cos \left( \alpha + \beta \right) = cos \alpha cos \beta - sin \alpha sin \beta$

Terbukti

Contoh Soal Penggunaan Rumus Jumlah Sudut Cosinus
Tentukan nilai cos $75^{o}$ !
Pembahasan:

$cos \; 75^{o} = cos \left( 45^{o} + 30^{o} \right)$

$cos \; 75^{o} = cos \; 45^{o} \cdot cos \; 30^{o} - sin \; 45^{o} \cdot sin \; 30^{o}$

$cos \; 75^{o} = \frac{1}{2} \sqrt{2} \cdot \frac{1}{2} \sqrt{3} - \frac{1}{2} \sqrt{2} \cdot \frac{1}{2}$

$cos \; 75^{o} = \frac{1}{4} \sqrt{6} - \frac{1}{4} \sqrt{2}$

$cos \; 75^{o} = \frac{1}{4} \left( \sqrt{6} - \sqrt{2} \right)$

Rumus Selisih Sudut Dua Cosinus

Rumus Selisih Dua Sudut Cos

Pembuktian rumus di atas dapat diperoleh dengan memanfaatkan rumus jumlah sudut cosinus yang telah kita buktikan terlebih dahulu. Caranya adalah dengan mengubah sudut $\beta$ menjadi sudut $- \beta$ . Untuk lebih jelasnya lihat langkah pembuktian di bawah.

Bukti:

$cos \left( \alpha - \beta \right) = cos \left( \alpha + (- \beta) \right)$

$cos \left( \alpha - \beta \right) = cos \alpha \cdot cos (- \beta) - sin \alpha \cdot sin (- \beta)$

$cos \left( \alpha - \beta \right) = cos \alpha \cdot cos \beta - sin \alpha \cdot -sin \beta$

$cos \left( \alpha - \beta \right) = cos \alpha \; cos \beta + sin \alpha \; sin \beta$

Terbukti

Contoh Soal Penggunaan Rumus Selisih Dua Sudut Cosinus
Tentukan nilai cos $75^{o}$ !
Pembahasan:

$cos \; 105^{o} = cos \left( 135^{o} - 30^{o} \right)$

$cos \; 105^{o} = cos \; 135^{o} \cdot cos \; 30^{o} - sin \; 135^{o} \cdot sin \; 30^{o}$

$cos \; 105^{o} = -\frac{1}{2} \sqrt{2} \cdot \frac{1}{2} \sqrt{3} - \frac{1}{2} \sqrt{2} \cdot \frac{1}{2}$

$cos \; 105^{o} = -\frac{1}{4} \sqrt{6} - \frac{1}{4} \sqrt{2}$

$cos \; 105^{o} = -\frac{1}{4} \left( \sqrt{6} - \sqrt{2} \right)$

Rumus Jumlah dan Selisih Dua Sudut Sinus

Rumus Jumlah Dua Sudut Sinus

Bukti:

$sin \left( \alpha + \beta \right) = cos \left( 90^{o} - (\alpha + \beta) \right)$

$sin \left( \alpha + \beta \right) = cos \left( (90^{o} - \alpha) - \beta \right)$

$sin \left( \alpha + \beta \right) = cos (90^{o} - \alpha) \cdot cos \beta + sin (90^{o} - \alpha) \cdot sin \beta$

$sin \left( \alpha + \beta \right) = sin \alpha \; cos \beta + cos \alpha \; sin \beta$

Contoh Soal Penggunaan Rumus Jumlah Sudut Sinus
Tentukan nilai dari $sin 105^{o} cos 75^{o} + cos 105^{o} sin 75^{o}$ !
Pembahasan:

$sin 105^{o} cos 75^{o} - cos 105^{o} sin 75^{o} = sin (105^{o} + 75^{o}$

$sin 105^{o} cos 75^{o} - cos 105^{o} sin 75^{o} = sin (180^{o}) = 0$

Rumus Selisih Dua Sudut Sinus

Bukti:

$sin \left( \alpha - \beta \right) = sin \left( \alpha + (- \beta) \right)$

$sin \left( \alpha - \beta \right) = cos \left( 90^{o} - (\alpha + (- \beta)) \right)$

$sin \left( \alpha - \beta \right) = cos \left( (90^{o} - \alpha) + \beta) \right)$

$sin \left( \alpha - \beta \right) = cos (90^{o} - \alpha) \cdot cos \beta - sin (90^{o} - \alpha) \cdot sin \beta$

$sin \left( \alpha - \beta \right) = sin \; \alpha \; cos \; \beta - cos \; \alpha \; sin \; \beta$

Contoh Soal Penggunaan Rumus Selisih Sudut Sinus
Tentukan nilai dari $sin 105^{o} cos 75^{o} + cos 105^{o} sin 75^{o}$ !
Pembahasan:

$sin 105^{o} cos 75^{o} - cos 105^{o} sin 75^{o} = sin (105^{o} - 75^{o}$

$sin 105^{o} cos 75^{o} - cos 105^{o} sin 75^{o} = sin (30^{o}) = \frac{1}{2}$

Rumus Jumlah dan Selisih Sudut Tangen

Rumus Jumlah Sudut Tangen

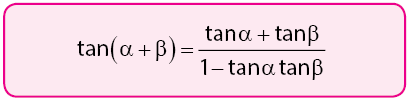
Rumus Jumlah Dua Sudut Tan

Bukti:

$tan(\alpha + \beta ) = \frac{sin(\alpha + \beta)}{cos(\alpha + \beta)}$

$tan(\alpha + \beta ) = \frac{sin \alpha \; cos \beta + cos \alpha \; sin \beta}{cos \alpha \; cos \beta - sin \alpha \; sin \beta}$

$tan(\alpha + \beta ) = \frac{\frac{sin \alpha}{cos \alpha} \cdot cos \alpha \; cos \beta + cos \alpha \; \frac{sin \beta}{cos \beta} \cdot cos \beta}{cos \alpha \; cos \beta - \frac{sin \alpha}{cos \alpha} \cdot cos \alpha \; \frac{sin \beta}{cos \beta} \cdot cos \beta}$

$tan(\alpha + \beta ) = \frac{tan \alpha \; cos \alpha \; cos \beta + cos \alpha \; tan \beta \; cos \beta}{cos \alpha \; cos \beta - tan \alpha \; cos \alpha \; tan \beta \; cos \beta }$

$tan(\alpha + \beta ) = \frac{cos \alpha \; cos \beta \left( tan \alpha + tan \beta \right)}{cos \alpha \; cos \beta \left( 1 - tan \alpha \; tan \beta \right)}$

$tan(\alpha + \beta ) = \frac{tan \alpha + tan \beta }{ 1 - tan \alpha \; tan \beta}$

Rumus Selisih Sudut Tangen

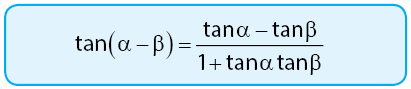
Rumus Selisih Dua Sudut Tan

Bukti:

Dengan menggunakan rumus jumlah sudut tangen yang telah di buktikan sebelumnya, pembuktian rumus selisih sudut tangen dapat diperoleh dengan mengganti sudut $\beta$ menjadi $- \beta$ .

$tan(\alpha - \beta ) = tan(\alpha + (-\beta))$

$tan(\alpha - \beta ) = \frac{tan \alpha + tan (-\beta)}{1 - tan \alpha tan (-\beta) }$

$tan(\alpha - \beta ) = \frac{tan \alpha - tan \beta}{1 + tan \alpha tan \beta }$

Terbukti

Contoh perhitungan selisih sudut Tangen
Jika diketahui $tan 35^{o} = 0,7$ dan $tan 72^{o} = 3,08$ , tentukan nilai $tan 107^{o}$ !
Pembahasan:

$tan 107^{o} = \frac{tan 35^{o} + tan 72^{o}}{1- tan 35^{o} \; tan 72^{o}}$

$tan 107^{o} = \frac{0,7 + 3,08}{1- 0,7 \cdot3,08}$

$tan 107^{o} = \frac{3,78}{-1,156} = 3,2699$

CONTOH SOAL

Berikut contoh soal yang berkaitan dengan rumus trigonometri jumlah dan selisih dua sudut.

Latihan 1
Diketahui cos α = 3/5 dan sin β = 5/13. Jika α adalah sudut lancip dan β sudut tumpul, tentukan nilai dari sin (α - β) !

Jawab :
α lancip berarti α berada di kuadran I.
β tumpul berarti β berada di kuadran II.

cos α = 3/5 → sin α = 4/5
sin α bernilai positif karena α berada di kuadran I.

sin β = 5/13 → cos β = -12/13
cos β bernilai negatif karena β berada di kuadran II.

sin (α - β) = sin α cos β - cos α sin β
sin (α - β) = 4/5 . (-12/13) - 3/5 . 5/13
sin (α - β) = -48/65 - 15/65
sin (α - β) = -63/65

Demikianlah pengertian dan rumus trigonometri jumlah dan selisih dua sudut yang bisa saya bagikan. Selamat belajar dan tetap semangat.

Wassalamualaikum Warohmatullohi Wabarokatuh

IDENTITAS TRIGONOMETRI PENJUMLAHAN DAN SELISIH DUA SUDUT

Kamis, 05 Agustus 2021

MODUL TRIGONOMETRI PENJUMLAHAN DAN SELISIH DUA SUDUT

1. Rumus Cosinus Jumlah dan Selisih Dua Sudut

mari kita simak rumus jumlah dan selisih dua sudut sinus dan cosinus beserta pembuktiannya.

Rumus Jumlah dan Selisih Sudut Cosinus

Rumus Jumlah dan Selisih Dua Sudut Sinus

Rumus Jumlah dan Selisih Sudut Tangen

Tidak ada komentar:

Posting Komentar

KUMPULA SOAL TRIGONOMETRI DARI TIM LAIN

Laporkan Penyalahgunaan